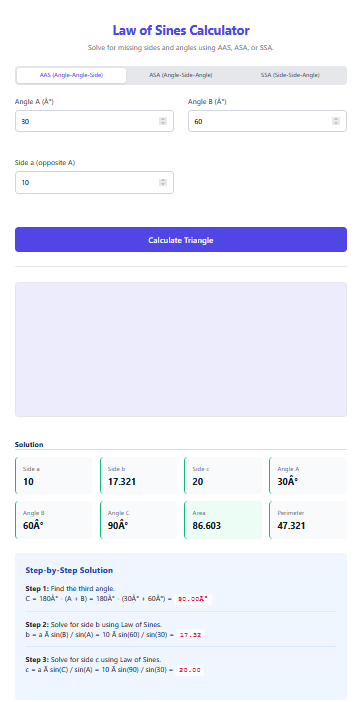
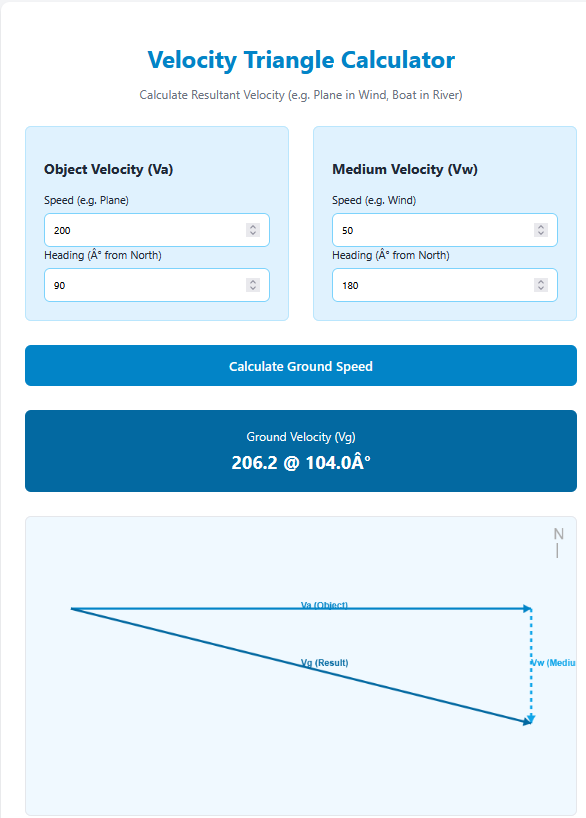
Knowing two angles and a side that is *not* between them is the AAS (Angle-Angle-Side) case. The AAS Triangle Calculator solves this by first finding the third angle (easy subtraction) and then using the Law of Sines to find the remaining side lengths.
Features
Non-Included Side: Specialized for when the side is opposite one of the known angles.
Fast 3rd Angle: Instantly computes the missing angle via the 180° rule.
Law of Sines Integration: Solves the ratios to find the missing sides.
Area & Perimeter: Automatically included in the final report.
How to Use This Calculator
Enter Angles: Input Angle A and Angle B.
Enter Side: Input Side a (which must be opposite Angle A for the labels to align, or just follow the non-included logic).
Calculate: The tool will deduce Angle C and Sides b & c.
Visualize: See the constructed triangle.
Formulas
The calculator uses the following mathematical principles:
Angle Sum: $$ C = 180 – A – B $$
Law of Sines: $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$
Area: $$ \text{Area} = 0.5 \cdot a \cdot b \cdot \sin C $$
Practical Applications
Surveying: Finding the height of a distant object (like a mountain) using two angle measurements from a baseline.
Astronomy: Parallax calculations.
Construction: Determining roof span lengths given pitch angles and one rafter length.
Tips for Success
Valid Angles: The sum of your two input angles must be less than 180.
Correspondence: Ensure you know which side corresponds to which angle for the Law of Sines to assign lengths correctly.
Congruence: AAS is a valid congruence theorem, meaning it always defines a unique triangle.
Frequently Asked Questions (FAQ)
Is this different from ASA?
Mathematically they are very similar, but the input setup differs (Non-Included vs Included side).
Can I solve for area?
Yes, once the sides are found via Law of Sines, area is calculated.
Final Words
From angles to answers. The AAS Triangle Calculator seamlessly converts partial angular data into a fully measured triangle, proving that you don’t need to measure every side to know everything about a shape.