In calculus and geometry, a Bounded Region is a finite area completely enclosed by a set of curves or lines. While standard integrals find the area under one curve, and “Area Between Curves” handles two, this calculator is designed for more complex regions defined by three distinct boundaries (like a triangle made of curves).
Finding this area manually requires finding all intersection points, splitting the integral into vertical slices, and carefully determining which function is “on top” for each slice. This tool automates the entire process.
Calculator Features
1. Triple Boundary Support
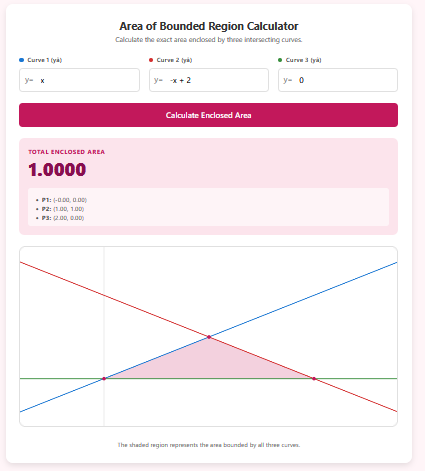
Enter three separate equations (y₁, y₂, y₃) to define your region. For example, entering y=x, y=-x+2, and y=0 defines a triangle with a base on the x-axis.
2. Automatic Vertex Detection
You do not need to calculate where the lines meet. The calculator runs a numerical search to find the three intersection points (vertices) that define the corners of the enclosed region.
3. Smart Region Identification
When three curves intersect, they partition the plane into many sections. Our algorithm intelligently identifies the central “bounded” region (the “curvilinear triangle”) by analyzing the median and minimum function values across the interval.
4. Detailed Vertex Reporting
The results section lists the exact coordinates (x, y) of the three vertices (P1, P2, P3), which is incredibly useful for checking your algebra homework.
Uses of Bounded Region Area
Optimization (Feasible Regions)
In linear and non-linear programming, the “feasible region” is bounded by multiple constraint lines. Calculating the area of this region can be useful for probability analysis within the constraint set.
Surveying and Land Area
Real-world plots of land are rarely defined by a single function. They are bounded by roads, rivers, and property lines. This calculator models such “irregular polygons” where sides can be curved.
Mechanical Engineering
Calculates properties of plates or laminates bounded by multiple machining paths (e.g., a bracket shape defined by three cutting curves).
Tips for Accurate Results
Ensure Intersections Exist
For a region to be “bounded,” the curves must actually cross each other. If y₁ and y₂ are parallel lines, they will never enclose a finite area with y₃ alone unless y₃ cuts both.
Check the Graph
The shaded pink region on the chart shows exactly what area is being calculated. If the wrong region is shaded, check your equations or try restricting the domain mentally to ensure you entered the intended curves.
Frequently Asked Questions (FAQs)
1. Can I use this for just 2 curves?
Technically, yes, but it is optimized for 3. For 2 curves (a “lens” shape), it is often easier to use our “Area Between Two Curves” calculator. If you use this one, set the 3rd curve to be a line that passes clearly “outside” the lens or intersects naturally.
2. What if my shape has 4 sides?
This calculator is specifically for 3-boundary regions / curvilinear triangles. For a 4-sided region, you can often split it into two 3-sided regions and add their areas.
3. Why are the vertices decimals?
The calculator uses numerical methods to find intersections. Even simple intersections like “sqrt(2)” will appear as 1.414… This is normal for computational tools.
4. Does order matter?
No. You can enter your boundaries in any order (y1, y2, y3). The algorithm sorts them automatically based on their values at each x-coordinate.
Final Words
Calculating the area of a region bounded by three curves is a classic challenge in calculus, requiring intuition about geometry and integration limits. The Area of Bounded Region Calculator automates the heavy lifting—finding intersections and setting up integrals—allowing you to focus on the result. Whether for optimization problems or geometric analysis, this tool provides the rigorous answers you need.