In calculus, a Definite Integral represents the accumulation of a quantity, such as the total distance traveled given a velocity function, or the area under a curve between two points a and b.
It is mathematically denoted as:
∫[a to b] f(x) dx
Unlike an “indefinite integral” which returns a function family (+C), a definite integral returns a specific number representing the “Net Signed Area”—where regions above the x-axis are positive and regions below are negative.
Calculator Features
1. Improper Integral Support (Infinity)
Most simple calculators fail when you try to integrate to infinity. Our tool includes dedicated buttons for -∞ and +∞, allowing you to evaluate improper integrals like ∫[0 to ∞] e^-x dx using advanced substitution techniques.
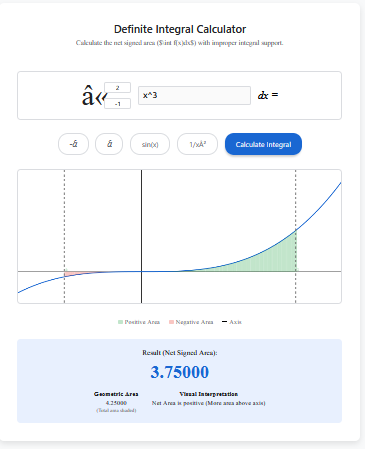
2. Net Signed Area vs. Geometric Area
The calculator provides two distinct results:
Result (Net Signed Area): The standard calculus result where negative areas subtract from the total.
Geometric Area: The total physical area shaded, treating all regions as positive.
3. Visual Area Interpretation
Calculus can be abstract, but our visualization makes it concrete. The graph explicitly colors positive regions in Green and negative regions in Red, helping students intuitively understand how cancellation occurs.
4. Built-in Math Engine
You don’t need to simplify your function before entering it. The text parser handles complex inputs like sin(x) + 1/x^2 directly.
Uses of Definite Integrals
Physics: Work and Energy
The definite integral is essential for calculating Work done by a variable force. For example, compressing a spring requires finding the integral of Hooke’s Law force over the distance compressed.
Probability: Normal Distribution
In statistics, finding the probability that an event occurs involves integrating the probability density function. Since the “tails” of a normal distribution go to infinity, our calculator’s improper integral feature is perfect for finding these probabilities.
Engineering: Center of Mass
To find the centroid or center of mass of a shape, engineers must calculate the definite integrals of the shape’s moment about the axes.
Tips for Calculation
Handling Discontinuities
If your function goes to infinity at a point inside your interval (like 1/x at x=0), the integral diverges. While our tool tries to handle large values, mathematically valid results require the interval to be continuous.
Using “inf” for Infinity
You can type “inf” or “-inf” directly into the limit boxes, or use the convenient buttons provided below the input fields.
Frequently Asked Questions (FAQs)
1. Why is my area negative?
A definite integral calculates “Net Signed Area.” If the curve spends more “time” below the x-axis than above it between intervals a and b, the result will be negative.
2. What is the difference between this and the Area Under Curve calculator?
While similar, this Definite Integral Calculator emphasizes the “Signed” nature of integration and specifically handles improper integrals (limits at infinity), whereas the Area Under Curve tool focuses more on geometric region visualization and absolute area.
3. Can it solve ∫ e^(-x^2) dx?
Yes. This is the Gaussian integral. Since it has no elementary antiderivative, our numerical approach is one of the only ways to evaluate it over specific limits.
4. How accurate is the “Infinity” calculation?
We use coordinate transformation (mapping the infinite range to a finite one like -π/2 to π/2) to evaluate these integrals with high precision, rather than just choosing a “large number” for the limit.
Final Words
The Definite Integral Calculator is a powerful companion for anyone studying calculus or applying it in scientific fields. By seamlessly handling improper limits and distinguishing between signed and total area, it clarifies concepts that often confuse students. Whether you are computing work in physics or probabilities in statistics, this tool ensures you get the rigorous, numeric answer you need.