An Enclosed Region is any 2D area completely bounded by a closed curve or a set of intersecting curves. While simple calculus problems often stick to “y as a function of x” (Cartesian coordinates), real-world shapes like planetary orbits, flower petals, or magnetic loops are often better described using Parametric or Polar equations.
This calculator is a universal tool that computes the area for all three major coordinate systems:
Key Formulas:
Cartesian: Area $A = \int_{a}^{b} |f(x) – g(x)| dx$
Polar: Area $A = \frac{1}{2} \int_{\theta_1}^{\theta_2} r(\theta)^2 d\theta$
Parametric (Green’s Theorem): Area $A = \frac{1}{2} \int_{t_1}^{t_2} (x(t)y'(t) – y(t)x'(t)) dt$
Calculator Features
1. Multi-Coordinate Support
Most calculators are limited to standard graphs. Ours lets you switch instantly between:
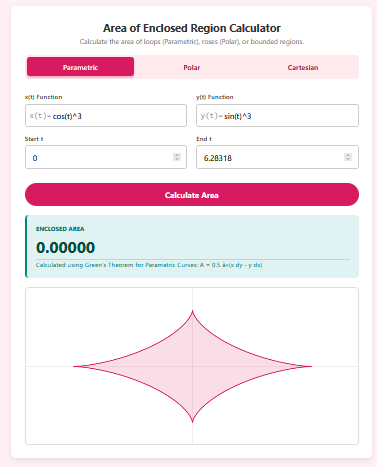
Parametric Mode: Perfect for loops like the astroid ($x=\cos^3 t$, $y=\sin^3 t$).
Polar Mode: Designed for radial shapes like rose curves ($r = \cos(k\theta)$).
Cartesian Mode: The classic area between two functions $f(x)$ and $g(x)$.
2. Green’s Theorem Integration
For parametric curves that form a closed loop, finding the area can be tricky with standard $y dx$ integration due to direction issues. Our engine uses the symmetric form of Green’s Theorem to ensure the area is calculated correctly regardless of the traversal direction (clockwise or counter-clockwise).
3. Dynamic Visualization
See exactly what you are calculating. The graph adapts to your mode—showing radial lines for Polar graphs or tracing the path for Parametric curves—so you can visually verify that the loop is closed.
Uses in Science and Engineering
Physics (Orbital Mechanics)
Planetary orbits are ellipses defined parametrically. Kepler’s Second Law states that a line joining a planet and the Sun sweeps out equal areas during equal intervals of time. This calculator can verify those swept areas.
Mechanical Engineering (Cams and Gears)
The profile of a cam or a gear tooth is often defined by parametric equations. Calculating the cross-sectional area is essential for determining the weight and moment of inertia of these rotating parts.
Antenna Design (Polar Patterns)
The radiation pattern of an antenna is typically plotted in polar coordinates. The “area” of the main lobe vs. side lobes helps engineers determine the directivity and efficiency of the antenna.
Tips for Accurate Results
Close the Loop
For Parametric and Polar calculations, ensure your start and end values ($t_1$ to $t_2$ or $\theta_1$ to $\theta_2$) complete a full cycle. For a standard circle or loop, this is usually $0$ to $2\pi$ ($6.283…$).
Watch for Self-Intersection
If a curve intersects itself (like a figure-eight), the “signed area” of the two lobes might cancel out. Our calculator takes the absolute value for the total region, but understanding your curve’s shape is key.
Frequently Asked Questions (FAQs)
1. Why is the Parametric area formula different?
In parametric calculus, $x$ and $y$ both depend on $t$. We cannot just integrate $y dx$ easily. Instead, we use the chain rule ($dx = x'(t) dt$) or Green’s Theorem to transform the integral into terms of $t$.
2. How do I calculate the area of a circle?
You can use any mode! In Cartesian: $y = \sqrt{r^2-x^2}$ (semicircle x 2). In Parametric: $x=r\cos(t), y=r\sin(t)$ from $0$ to $2\pi$. In Polar: $r = constant$ from $0$ to $2\pi$. All will yield $\pi r^2$.
3. What is a “Rose” curve?
A rose is a polar graph of the form $r = \cos(k\theta)$. If $k$ is an integer, it creates petals. Use the Polar mode to find the area of one petal or the entire flower.
4. Can I enter “pi”?
Yes, simply type “pi” in the input fields. The calculator recognizes it as $3.14159…$
Final Words
The Area of Enclosed Region Calculator removes the boundaries of coordinate systems. By seamlessly handling Cartesian, Parametric, and Polar equations, it empowers you to tackle the most complex geometric problems found in advanced calculus and physics. Whether you are analyzing a simple parabola or a complex magnetic field loop, this tool provides the precision and flexibility you need.