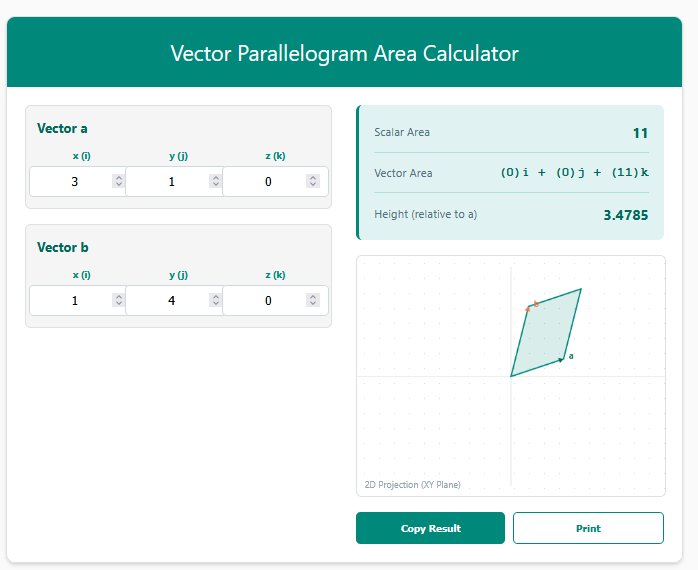
The Vector Parallelogram Area Calculator demonstrates one of the most fundamental properties of vector mathematics: the magnitude of the cross product of two vectors exactly equals the area of the parallelogram they span.
Unlike the triangle calculator, which divides the result by 2, this tool gives you the full area magnitude, making it essential for physics problems involving “flux per unit area” or stress tensors.
Calculator Features
1. Full Parallelogram Solver
Simply input vectors $\vec{a}$ and $\vec{b}$ to instantly get the area of the 4-sided shape they form. No need to calculate base and height manually.
2. Height Calculation
A unique feature of this tool is that it works backwards to tell you the “height” of the parallelogram relative to Vector A. This is equivalent to finding the perpendicular distance.
3. Vector & Scalar Outputs
It provides both:
Scalar Area: The physical size (e.g., $50 m^2$).
Vector Area: The directional area components $(S_x)i + (S_y)j + (S_z)k$.
The Math
Area Formula
The area is simply the magnitude of the cross product:
Area = $|\vec{a} \times \vec{b}|$
Height Formula
Since $Area = Base \times Height$, and the geometric base is the length of vector $\vec{a}$ ($|\vec{a}|$):
$Height = \frac{|\vec{a} \times \vec{b}|}{|\vec{a}|}$
Real-World Applications
Crystallography
In material science, the “Unit Cell” of a crystal lattice is often a parallelepiped. Calculating the area of its faces is the first step to determining density and atomic packing.
Computer Graphics (Texture Mapping)
Textures are often mapped onto surfaces using “UV mapping,” which relies on understanding the area deformation of parallelogram grid squares.
Mechanical Torque
While not an area, Torque ($\tau = \vec{r} \times \vec{F}$) shares the exact same math. This calculator can technically compute the magnitude of torque if you input the radius and force vectors!
Tips
Triangle Connection
Need the area of the triangle formed by these vectors? Just take the result from this calculator and divide it by 2.
Checking Perpendicularity
If the calculated Area equals $|\vec{a}| \times |\vec{b}|$ exactly, it means your vectors are perfectly perpendicular ($90^\circ$), forming a Rectangle.
Frequently Asked Questions (FAQs)
1. Can I use this for a Rhombus?
Yes! A rhombus is just a special parallelogram where $|\vec{a}| = |\vec{b}|$. The formula works perfectly.
2. Why calculate “Height”?
Often in physics, you know the force (Area term) and the lever arm (Base), and you need to find the effective perpendicular component (Height).
3. What does a negative component mean?
In the Vector Area output, a negative component (like $-5k$) simply means the normal vector points in the negative Z direction.
Final Words
The Vector Parallelogram Area Calculator is a fundamental utility for anyone working with vector calculus. By visualizing the cross product as a geometric area, it creates a bridge between abstract algebra and tangible shape properties.