Finding the area of a triangle is often more than just ‘base times height’. In the real world—and in advanced geometry—you don’t always have those two simple numbers. You might have three side lengths (Heron’s Formula), two sides and an angle (SAS), or even just three coordinate points on a graph (Shoelace Formula). Our Area of Triangle Calculator is an all-in-one powerhouse designed to handle every possible scenario, turning complex trigonometry and algebra into a single click.
Whether you are a land surveyor calculating a plot size or a student tackling a geometry proof, this tool adapts to the data you have, ensuring you never have to scramble for the right formula.
Calculator Features & Modes
We have broken down the calculator into intuitive tabs, each dedicated to a specific geometric method:
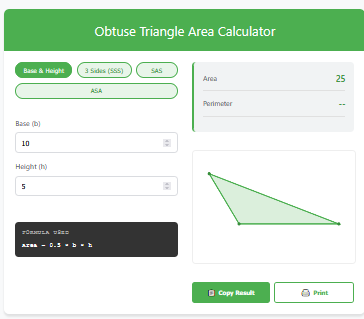
1. Base & Height (Classic)
The standard . Perfect for simple textbook problems or right triangles where the dimensions are obvious.
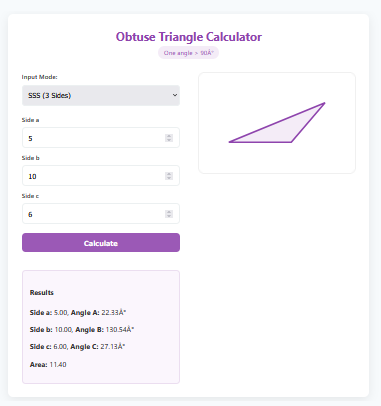
2. SSS (Heron’s Formula)
Don’t know the height? No problem. If you can measure all three sides ($a, b, c$), the calculator uses Heron’s Formula: . This is incredibly useful in construction where measuring diagonal lengths is easier than finding a perpendicular height.
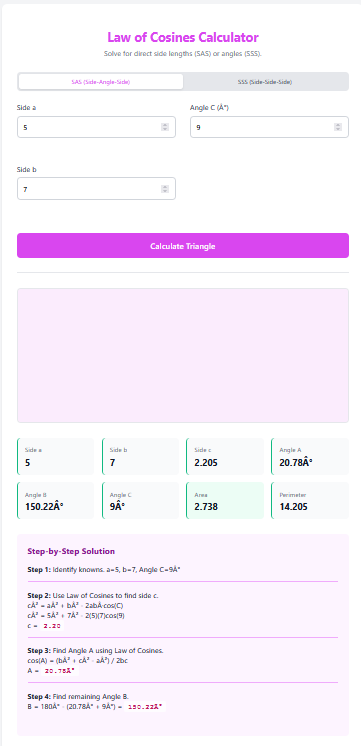
3. SAS and ASA (Trigonometry)
Sometimes you can’t reach all sides.
– SAS: Uses two sides and the included angle ($ \frac{1}{2}ab\sin(C) $).
– ASA: Uses two angles and the side between them.
Great for surveying where you can measure a baseline and shoot angles to a distant point.
4. Coordinate Geometry (Vertices)
A favorite for engineers and computer graphics. Simply input the $(x, y)$ coordinates of the three corners, and the calculator applies the Shoelace Formula to determine the area precisely.
Real-World Applications
Land Surveying & GIS
Land plots are rarely perfect rectangles. Surveyors break irregular fields into a series of triangles (triangulation) and use Heron’s Formula or GPS coordinates (Shoelace Formula) to calculate the total acreage with extreme precision.
Architecture and Design
From triangular truss systems to modern A-frame houses, architects need to know the surface area of triangular sections to estimate materials for roofing, siding, and insulation.
Computer Graphics
Every 3D model in your favorite video game is made of thousands of tiny triangles (polygons). The graphics card constantly calculates vertex positions and areas to render light and texture correctly.
Tips for Accurate Results
Triangle Inequality: For SSS mode, remember that any two sides added together must be longer than the third side. If you enter 2, 2, and 10, the triangle cannot exist!
Angle Units: For SAS and ASA, ensure your angles are measuring what you think they are. Our calculator uses Degrees (standard 0-360), not Radians.
Precision: Coordinate calculations can be sensitive. Double-check your signs (negative coordinates) as a flipped sign moves a point to a completely different quadrant.
Frequently Asked Questions (FAQ)
1. Can I calculate the area of a 3D triangle?
This calculator is for 2D plane geometry. For 3D space, you would typically use the cross product of two vectors, which is a more advanced vector calculus method.
2. Why does the Coordinate mode give a positive area even if I start counter-clockwise?
The Shoelace formula mathematically can result in a negative number depending on the order of points (clockwise vs counter-clockwise). Our calculator automatically takes the absolute value, ensuring the physical area is always positive.
3. What is the ‘Semi-perimeter’?
The semi-perimeter ($s$) is simply half of the perimeter ($s = \frac{a+b+c}{2}$). It is a crucial intermediate step in Heron’s Formula but has little physical meaning on its own.
Final Words
Triangles are the simplest polygons, but calculating their area can be surprisingly complex depending on what information you have. The Area of Triangle Calculator bridges the gap between basic geometry and advanced trigonometry. By offering five distinct solving modes, it ensures that no matter how your problem is presented, you have the tool to solve it instantly and accurately.