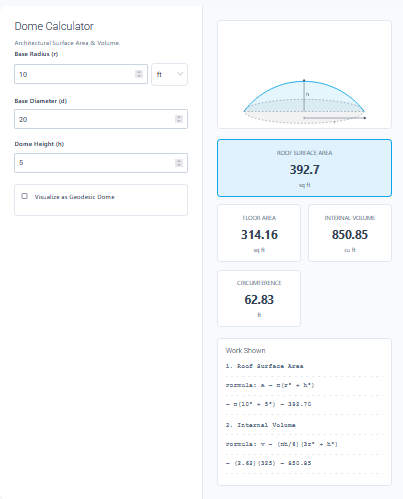
Kite Area Calculator
In geometry, a Kite is a quadrilateral with two distinct pairs of equal-length sides that are adjacent to each other. It looks exactly like the classic toy you fly in the park. Key geometric features include:
- Diagonals that intersect at 90 degrees (Perpendicular).
- One axis of symmetry (the main diagonal).
- One pair of opposite angles that are equal.
The Kite Area Calculator allows you to compute the surface area using whichever variables you have: Diagonals, Side lengths, or Coordinates.
Ways to Calculate Area
1. The Diagonals Method (Standard)
This is the most common and simplest method. Because the diagonals are perpendicular, the area is half their product.
- Formula:
- Where: and are the lengths of the Long and Short diagonals.
2. Trigonometry (SAS)
If you know the lengths of the two unequal sides ( and ) and the angle () between them (where they meet at the unequal axis), you can treat the kite as two identical triangles.
- Formula:
3. Coordinate Geometry
If the kite is mapped on a grid (X,Y plane), use the Shoelace Formula.
- Method: Enter coordinates for vertices .
Practical Uses
Kite Making & Aerodynamics
For a kite to fly, the Lift-to-Drag Ratio must be correct. Lift is directly proportional to Surface Area. A hobbyist building a stunt kite needs to calculate the exact area of ripstop nylon fabric required, and how that area relates to the weight of the frame sparring.
Architecture & Tiling
The "Deltoid" (kite shape) is used in Penrose Tiling and decorative mosaics. Calculating the area of individual tiles helps estimates for grout and ceramic quantities.
Jewelry Design
The "Kite Cut" is a fancy diamond shape often used for side stones or drop earrings. The surface area of the table (top face) affects the gem's brilliance and light return.
Frequently Asked Questions (FAQ)
Is a Rhombus a Kite?
Yes! A Rhombus is a *special* kite where all four sides are equal length. The diagonal formula () works perfectly for a Rhombus, too.
Is a dart a kite?
Yes. A "Dart" is a concave kite (it looks like an arrowhead, with one interior angle > 180 degrees). Our calculator works for convex kites (standard) and concave darts correctly.
How do I find diagonals if I only have sides?
You cannot find the diagonals with *only* the side lengths because the kite could be "squashed" or "stretched." You need at least one internal angle to lock the shape's geometry.
Final Words
Whether designing a high-speed foil or cutting a precious stone, the kite is a shape of dynamic balance. The Kite Area Calculator ensures your measurements fly straight and true.