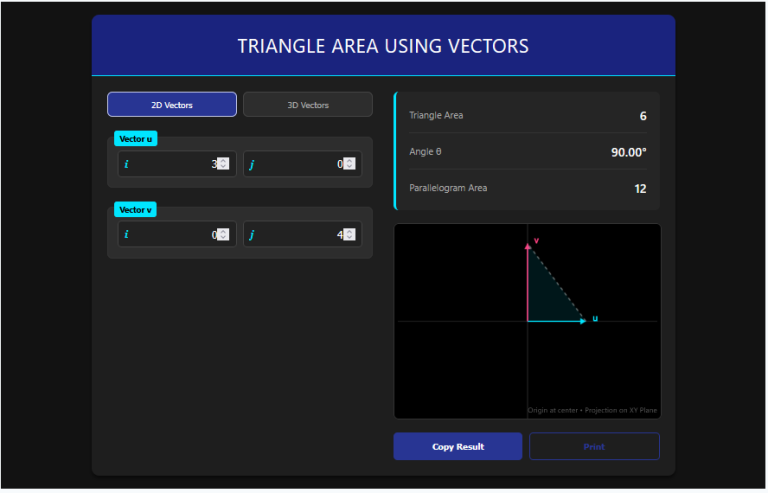
A Limaçon (French for "snail") is a fascinating polar curve defined by the equation . Depending on the ratio of to , it can be a simple dimpled loop, a heart shape (Cardioid), or a shape with a distinct inner "loop-the-loop."
The Limacon Area Calculator is an advanced calculus tool that computes the area enclosed by this polar curve. Uniquely, it can distinguish between the "Inner Loop" area and the "Area Between Loops," solving the definite polar integral automatically.
Features
1. Polar Graphing: Instantly draws the curve (or ), visualizing the specific shape (looped, cardioid, or convex).
2. Region Selection: Allows you to calculate specific theoretical areas:
- Total Area: The full integral form.
- Inner Loop: Specifically isolates the area of the small inner loop (exists when ).
- Between Loops: Calculates the area of the outer shell excluding the inner hole.
3. Step-by-Step Integral: Displays the integration limits (values of ) used to find the loop, aiding calculus students in homework verification.
4. Shaded Visualization: Highlights the exact region being calculated on the graph in red.
Uses
- Calculus Students: Verifying answers for polar area integration problems.
- Physics & Engineering: Modeling camera lens characteristics, microphone pickup patterns (cardioid), or cam mechanisms.
- Graphic Design: Generating precise mathematical curves for logos or art.
Tips
- The "a/b" Ratio:
- If : You get an inner loop.
- If : You get a Cardioid (Heart).
- If : You get a dimpled bean shape (no loop).
- If : The shape becomes convex (egg-like).
- Symmetry: Cosine limacons are symmetric across the X-axis. Sine limacons are symmetric across the Y-axis. The area is identical, just rotated.
FAQs
What is the area formula?
The area is found using the polar integral formula: .
Why is the inner loop separate?
Mathematically, the inner loop is formed when becomes negative. In many physical applications, this "negative radius" region is distinct from the main body.
Does calculating "Total" sum them up?
The integral from 0 to sums the geometric area swept by the radius. For a looped limacon, this effectively calculates because the loop is traversed twice? No, actually, the integral calculates the area of the surface "swept" by the radius. Be careful with definitions in problem sets!
Final Words
From the classic heart-shaped Cardioid to the complex looped Limaçon, these curves are beautiful examples of polar geometry. This calculator takes the pain out of the integration, letting you focus on the shape's properties and applications.