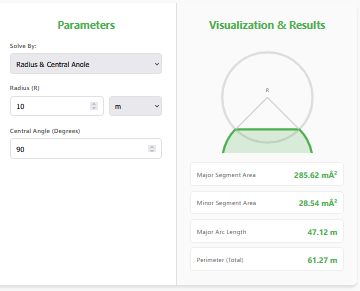
A Major Sector is what remains of a pizza after you take a slice out. Mathematically, it is a sector with a central angle greater than $180^\circ$.
While most textbooks focus on the “Minor Sector” (the slice), real-world applications often require measuring the “Major Sector” (the rest of the pie), such as in land surveying or rotational mechanics.
Calculator Features
1. Reflex Angle Support
Standard calculators break if you enter an angle larger than $180^\circ$. Our tool is built specifically for “Reflex Angles” ($180^\circ < \theta < 360^\circ$), allowing you to calculate the large area directly.
2. Complementary Logic
Don’t know the big angle? No problem. You can enter the “Missing Slice Angle” (Minor Angle), and the calculator will automatically subtract it from $360^\circ$ to find the Major Sector properties.
3. Full Geometry Suite
Along with Area, it calculates:
Major Arc Length: The distance around the curved “Pac-Man” back.
Perimeter: The total boundary length, including the two radii.
Formulas
The formulas are identical to the standard sector formulas, but we use the Reflex Angle ($\theta_{major}$).
Area
Area = \frac{\theta_{major}}{360} \times \pi r^2
Arc Length
Arc Length L = \frac{\theta_{major}}{360} \times 2 \pi r
Perimeter
Perimeter P = L + 2r
Real-World Applications
Security Cameras
Wide-angle security cameras often cover a “Major Sector” field of view (e.g., $270^\circ$ around a building corner). Installers calculate this area to determine blind spots.
Mechanical Engineering (Cams)
In cam design, the “dwell” period might correspond to a minor sector, while the “action” period covers the major sector of the cam’s rotation.
Pac-Man Design
The iconic Pac-Man shape is a dynamic Major Sector. As his mouth opens and closes, the central angle changes, altering his area and perimeter.
Tips
The “Missing Slice” Trick
It is often easier to measure the small missing slice than the massive remaining shape. Measure the small angle, enter it into the “Minor Angle” mode, and let us do the math.
Visual Check
Always check the visual preview. A Major Sector should look like a circle with a wedge missing. If it looks like a wedge, you are calculating a Minor Sector.
Frequently Asked Questions (FAQs)
1. Can I use this for a Semicircle?
Yes. A semicircle is both a Major and Minor sector with an angle of $180^\circ$. The formula works perfectly.
2. How do I convert from Percentage?
If you know the sector is $75\%$ of the circle, multiply $360 \times 0.75 = 270^\circ$ to get the angle.
3. Why is perimeter $L + 2r$?
To walk around the entire shape, you must walk along the curved back ($L$), then in to the center ($r$), and back out to the edge ($r$).
Final Words
The Major Sector Area Calculator helps you see the bigger picture. By focusing on the “rest of the pie,” it solves problems that standard calculators miss, ensuring you have the right tool for every angle between $181^\circ$ and $360^\circ$.