A Major Segment is the larger portion of a circle when it is cut by a chord. While the “Minor Segment” is the small crust, the Major Segment is the rest of the pie—always covering more than 50% of the circle’s area.
This calculator is designed to solve for this larger area specifically, which is often needed in tank volume calculations and architectural design where the “main body” is the focus, not the cutoff.
Calculator Features
1. Complementary Calculation
Most geometry textbooks only give formulas for the minor segment. This tool automatically performs the “Area of Circle minus Area of Minor Segment” logic for you, saving you the extra subtraction step.
2. Flexible Inputs
You can define the cut using any of the standard parameters:
Central Angle: The angle of the “missing” wedge.
Chord Length: The width of the straight cut.
Height (Sagitta): The depth of the minor cut.
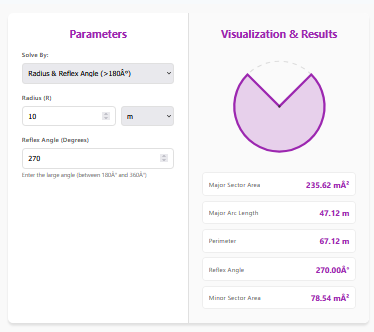
3. Dynamic Visualization
The tool renders the Major Segment in green, making it visually clear that you are calculating the “big” part of the circle. This prevents the common error of mixing up major and minor areas.
Formulas
The easiest way to find the Major Segment Area ($A_{major}$) is to subtract the Minor Segment Area ($A_{minor}$) from the Total Circle Area.
Total Area
Area_{Total} = \pi R^2
Minor Segment Area
A_{minor} = \frac{1}{2} R^2 (\theta – \sin \theta)
Where $\theta$ is the central angle of the minor sector in radians.
Major Segment Area (Final)
A_{major} = \pi R^2 – A_{minor}
Alternative (Direct Formula)
You can also calculate it directly using the reflex angle ($2\pi – \theta$):
A_{major} = \frac{1}{2} R^2 ((2\pi – \theta) + \sin \theta)
Practical Applications
Liquid Storage
If a cylindrical oil tank is more than half full, the cross-section of the oil is a Major Segment. Engineers needs this area to calculate the total volume of fuel.
Interior Design (Round Tables)
If you cut a small flat edge on a circular table to fit it against a wall, the remaining table surface (the usable part) is a Major Segment.
Tunneling
Road tunnels are often circular. The “roadway” cuts off a bottom segment (for drainage/utilities), leaving the main air space above as a Major Segment.
User Tips
Defining the Cut
When entering the “Height” or “Angle”, you are usually defining the properties of the *cut* (the minor part). The calculator assumes this convention to find the remaining major area.
Unit Management
The tool supports instant unit conversion. You can input Radius in meters but get the Area in square feet simply by selecting the dropdown options.
Frequently Asked Questions (FAQs)
1. What if the chord is the diameter?
Then the circle is cut exactly in half. Both the Major and Minor segments are Semicircles. The area is $\frac{1}{2} \pi R^2$.
2. Can I enter the Reflex Angle directly?
Currently, the tool expects the standard central angle ($< 180^\circ$) or chord properties. Entering a reflex angle ($> 180^\circ$) might be interpreted as the minor angle of the other side, which gives the same geometry but is less standard.
3. Is perimeter the circumference?
No. The perimeter of a major segment includes the long arc length PLUS the chord length. It is the distance around the entire shape.
Final Words
Whether you are calculating fuel in a tank or designing a custom window, the Major Segment Area Calculator ensures you focus on the “big picture”—the main body of the circle—without getting lost in subtraction errors.