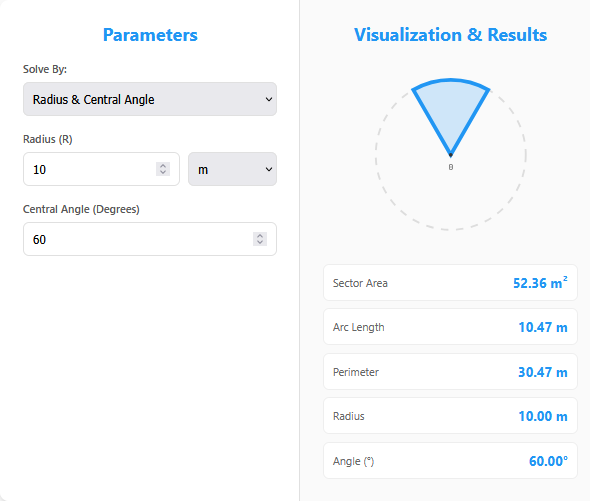
A Sector is what most people call a “slice of pizza.” It is the region bounded by two radii and an arc. A “Minor Sector” specifically refers to a slice smaller than a semicircle (Angle < 180°).
Calculating this area is one of the most common tasks in geometry, used everywhere from pie chart creation to mechanical engineering cam design.
Calculator Features
1. Three-Way Solver
Often you don’t have all the variables. This calculator solves the triangle of variables (Radius, Angle, Arc Length) if you know any two:
Radius & Angle: The standard classroom problem.
Radius & Arc Length: If you measured the curved outer edge.
Arc Length & Angle: If you don’t know the radius, the tool reverse-engineers it.
2. Instant Arc & Perimeter
Beyond the Area, the tool instantly computes the Arc Length ($L$) and the total Perimeter ($2r + L$). This is crucial for material usage when framing a curved shape.
3. Smart Visuals
The SVG visualizer dynamically adjusts the wedge size. If your parameters define a full circle or a tiny sliver, the diagram reflects reality immediately.
Formula for Sector Area
The formula is intuitive: it is simply a fraction of the full circle’s area.
Let $r$ be the radius and $\theta$ be the central angle in degrees.
Area
Area $A = \frac{\theta}{360} \times \pi r^2$
Using Radians
A = \frac{1}{2} r^2 \theta_{rad}$
Arc Length
Arc Length $L = \frac{\theta}{360} \times 2 \pi r$
Real-World Applications
Data Visualization
Pie Charts are sectors. The angle of each slice is proportional to the data percentage. A $25\%$ share means a $90^\circ$ sector.
Irrigation
Center-pivot irrigation systems water fields in a circular pattern. Usually, they run in a partial circle (a sector), and farmers need to calculate the acreage covered.
Fashion Design
Circular skirts (skater skirts) are cut from fabric as a large sector (often a “donut” sector). Pattern makers use sector formulas to calculate the waist radius.
Important Notes:
Perimeter Trap
Don’t confuse “Arc Length” with “Perimeter”. The Arc Length is just the curved part. The Perimeter includes the two straight sides (radii) as well. The calculator shows both distinguishingly.
Degrees vs Radians
This calculator is set to Degrees (e.g., $90^\circ$). If your homework gives you Radians (e.g., $\frac{\pi}{2}$), convert it first: $Degrees = Radians \times \frac{180}{\pi}$.
Frequently Asked Questions (FAQs)
1. What if my angle is > 180?
That creates a “Major Sector” (like Pac-Man). The formula is exactly the same, but computationally it is termed “Major”. We have a dedicated Major Sector Calculator as well.
2. How do I find the radius if I only have Area and Angle?
Rearrange the formula: $r = \sqrt{\frac{360 \times Area}{\pi \times \theta}}$.
3. Can I calc area with just Arc Length ($L$) and Radius?
Yes! The simplified formula is $Area = \frac{1}{2} \times r \times L$. This works without knowing the angle!
Final Words
The Minor Sector Area Calculator takes the headache out of fractions of circles. Instead of manually dividing $360$ degrees, simply punch in your parameters and get the precise area, arc, and perimeter instantly.