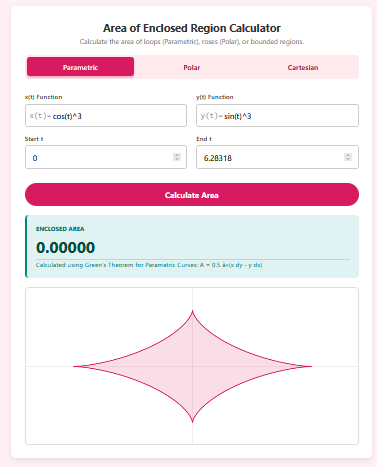
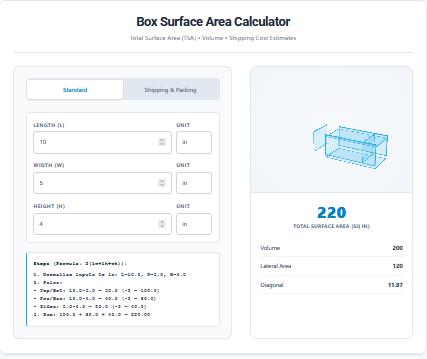
Parallelogram Calc
In analytic geometry, a parallelogram is defined not just by sides and angles, but by vertices on a Cartesian plane . This approach is essential for computer graphics, GPS mapping, and vector physics.
The Parallelogram Coordinates Calculator allows you to input the coordinates of the vertices to instantly find the Area, Perimeter, and verify geometric properties using the Shoelace Formula and Distance Formula.
How to Use This Calculator
Enter the X and Y coordinates for the four corners of your shape:
- Vertex A:
- Vertex B:
- Vertex C:
- Vertex D:
Note: The calculator will automatically check if the points actually form a parallelogram (opposite sides are parallel and equal).
Formulas Used
1. The Shoelace Formula (Area)
Instead of base x height, which is hard to find on a slanted grid, we use the determinant method:
- Area:
It calculates the “signed area” by cross-multiplying coordinates and taking the absolute value.
2. Distance Formula (Perimeter)
We calculate the length of each side using Pythagoras:
- Length AB:
The totals are summed to get the Perimeter.
Why Coordinates?
Computer Graphics (GIS)
In games and mapping software, shapes are stored as lists of coordinates. To render a texture onto a slanted wall, the physics engine calculates the area of the parallelogram formed by the vertices.
Land Surveying
Surveyors do not measure “base and height.” They measure GPS waypoints. This calculator converts those raw latitude/longitude points (mapped to a grid) into usable acreage.
Vector Physics
The area of a parallelogram defined by two vectors and represents the magnitude of their Cross Product. This acts as a measure of torque or rotational force.
Frequently Asked Questions (FAQ)
1. How do I know if it is a valid parallelogram?
The diagnonals must bisect each other. That means the midpoint of diagonal AC must be exactly the same as the midpoint of diagonal BD. Our calculator checks this for you.
2. Does the order of points matter?
Yes! You must list them in order around the perimeter (e.g., clockwise). If you jump across the shape (A to C), the Shoelace formula will fail and give you a “self-intersecting” bowtie shape.
3. Can I use negative coordinates?
Absolutely. The formulas work in all four quadrants of the graph.
Final Words
When you leave the drafting table and enter the digital grid, you need more than a ruler. The Parallelogram Coordinates Calculator brings algebraic precision to geometric shapes.