For many, the word ‘trigonometry’ brings back memories of confusing equations and abstract symbols. But at its core, trigonometry is simply the study of triangles and how their side lengths relate to their angles. It is the mathematical bridge between linear measurement (how far) and angular measurement (what direction). Our Right Triangle Trigonometry Calculator bridges this gap for you, turning complex SOH CAH TOA problems into instant, understandable solutions.
Whether you are a pilot calculating a flight path, a physics student assessing forces, or just trying to measure the height of a tree without climbing it, this tool is your digital assistant. It doesn’t just give you the answer; it breaks down the relationships between Sine, Cosine, and Tangent, helping you learn as you solve.
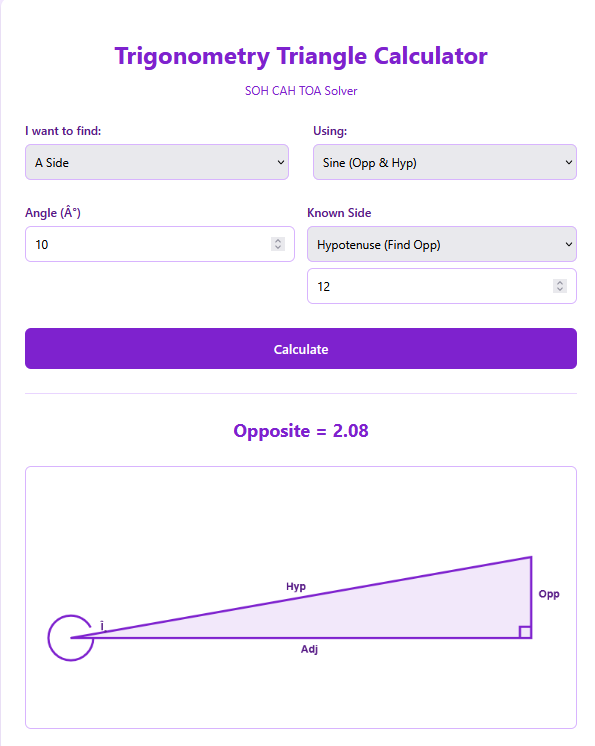
Understanding SOH CAH TOA
Before diving into the calculator’s features, it is helpful to look at the three pillars of right triangle trig. These acronyms are your roadmap:
SOH: Sine = Opposite / Hypotenuse
CAH: Cosine = Adjacent / Hypotenuse
TOA: Tangent = Opposite / Adjacent
Our calculator explicitly labels these sides based on the angle you are looking at, eliminating the common confusion of ‘which side is adjacent?’.
Calculator Features
Interactive Angle Perspective
One of the hardest parts of trig is realizing that ‘Opposite’ and ‘Adjacent’ change depending on which angle you are standing at. Our tool features an interactive visual where you can click on Angle $\alpha$ (top) or Angle $\beta$ (bottom). As you switch, the text labels on the triangle update instantly, reinforcing that the side opposite to $\alpha$ is adjacent to $\beta$.
Complete Trigonometric Breakdown
Calculators often just spit out a number. Ours provides a Step-by-Step Trig Breakdown. It lists the specific Sin, Cos, and Tan values for both acute angles in the triangle. This is invaluable for students who need to show their work or verify manual calculations.
Flexible Input Modes
Real life problems don’t always come in the same format. We support:
Two Legs: Input the two straight sides to find the hypotenuse and all angles.
Hypotenuse & Leg: Classic Pythagorean setup.
Angle & Side: The true power of trig—finding physical lengths from a single measurement and a known angle (like a shadow length and sun angle).
Real-World Applications
Trigonometry effectively runs the modern world. Here are fascinating ways it is used:
Aviation and Flight
Pilots live and breathe trigonometry. When a plane needs to land, it follows a ‘glide slope’—typically a 3-degree angle. Using the altitude (Opposite side) and the angle (3°), they calculate the distance to the runway (Adjacent side). Similarly, if a wind is blowing the plane sideways, they use trig vectors to calculate the correct ‘crab angle’ to stay on course.
Forensics
Crime scene investigators use trigonometry to analyze blood spatter. By measuring the width and length of a blood droplet, they can calculate the angle of impact . This helps reconstruct exactly where a victim was standing when an event occurred.
Physics and Engineering
Any force that acts at an angle—like pushing a lawnmower or pulling a sled—is split into vertical and horizontal components using Sine and Cosine. Engineers calculate these ‘vectors’ to ensure bridges don’t collapse and buildings withstand wind loads.
Tips for Success
Check Your Mode: Calculators can read angles in Degrees or Radians. Our tool uses Degrees by default, which is standard for most practical construction and navigation tasks.
Hypotenuse is Key: Remember, the Hypotenuse is *always* the denominator in Sine and Cosine. It is never used in Tangent (TOA).
Inverse Functions: If you know the ratio (e.g., Opp/Hyp = 0.5) and need the angle, you use the inverse function ($\{sin}^{-1}$). Our calculator handles this automatically when finding angles.
Frequently Asked Questions (FAQ)
1. Why is Tangent of 90 degrees undefined?
Tangent is Opposite/Adjacent. As an angle approaches 90°, the Opposite side gets huge and the Adjacent side gets tiny. At exactly 90°, the Adjacent side becomes zero. Division by zero is impossible in standard math, hence it is undefined.
2. What is the difference between Sin and Cos?
They are complements! The Sine of an angle is equal to the Cosine of its complement ($90 – \text{angle}$). If $\sin(30°) = 0.5$, then $\cos(60°) = 0.5$.
3. Can I use this for non-right triangles?
Not directly. SOH CAH TOA only works for right triangles. For non-right triangles, you would need the Law of Sines or Law of Cosines calculators.
Final Words
Trigonometry is the language of triangles, allowing us to translate between angles and distances. With the Right Triangle Trigonometry Calculator, you don’t need to memorize tables or struggle with scientific calculator buttons. You get extended insights, visual aids, and instant accuracy. Whether analyzing a crime scene or just finishing homework, let the power of SOH CAH TOA work for you.