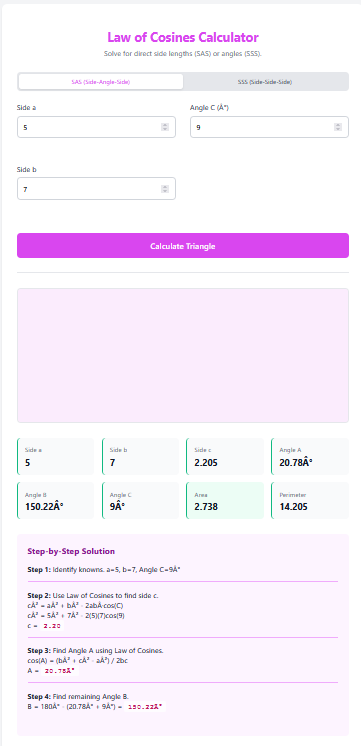
When you know two sides and the angle pinned between them, you have a classic SAS (Side-Angle-Side) scenario. The SAS Triangle Calculator uses the Law of Cosines to bridge the gap, calculating the missing third side and the remaining two angles with ease.
Features
Included Angle Logic: specifically designed for the setup where the angle is between the known sides.
Law of Cosines: Calculates the missing side length $c$ first.
Full Profile: Solves for the remaining two angles to complete the 180° set.
Dynamic Visual: Draws the triangle with the known angle at the origin for clear understanding.
How to Use This Calculator
Identify Inputs: Ensure your angle is the “included” one (between the two sides).
Enter Data: Input Side a, Side b, and Angle C.
Calculate: Find the length of Side c and the other angles.
Use Results: Apply the calculated dimensions to your project.
Formulas
The calculator uses the following mathematical principles:
Law of Cosines (for Side): $$ c^2 = a^2 + b^2 – 2ab\cos C $$
Law of Sines: Used to find the smaller of the remaining angles to ensure stability.
Area: $$ \text{Area} = 0.5 \cdot a \cdot b \cdot \sin C $$
Practical Applications
Navigation: Calculating direct distance to a destination given a turn angle and distance traveled on two legs.
Surveying: Triangulation from a known baseline and measured angle.
Robotics: Calculating the position of an end-effector arm given link lengths and joint angle.
Tips for Success
Angle Unit: Input is in degrees.
Unique Solution: SAS always produces exactly one unique triangle answer.
Orientation: The visualization places the known angle at the bottom-left or origin for clarity.
Frequently Asked Questions (FAQ)
What if the angle is not between the sides?
Then use the SSA (Side-Side-Angle) Calculator, as that is a different geometric case.
Can it solve for area?
Yes, the SAS formula for area is extremely direct and provided in the results.
Final Words
Close the gap in your geometry. The SAS Triangle Calculator perfectly connects two sides and an angle to reveal the full picture, making it indispensable for navigation and design.