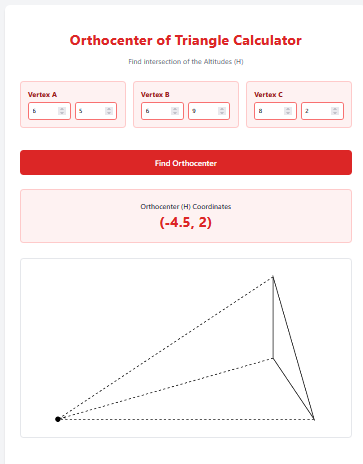
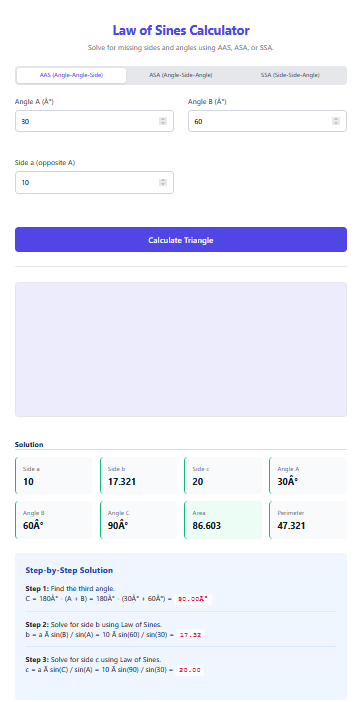
A Scalene Triangle has NO equal sides and NO equal angles. It is the most common ‘random’ triangle found in nature and surveying. The Scalene Triangle Calculator uses the powerful Heron’s Formula to calculate the Area directly from the three side lengths, without needing to know any angles or height.
Features
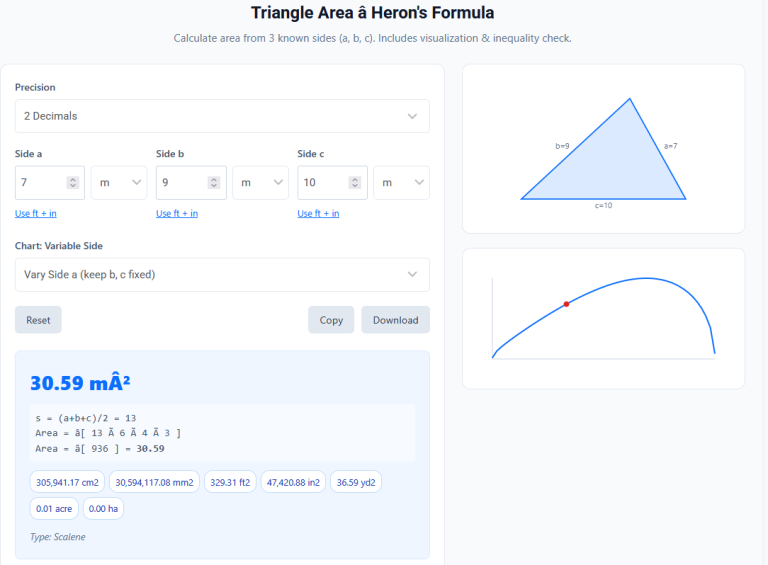
Heron’s Formula Engine: Calculates area purely from $s_1, s_2, s_3$.
Validity Check: Ensures $a+b>c$ to prevent invalid inputs.
Semi-Perimeter: specific output for the ‘s’ value used in the formula.
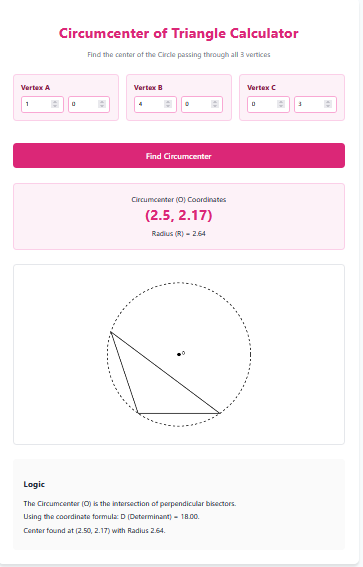
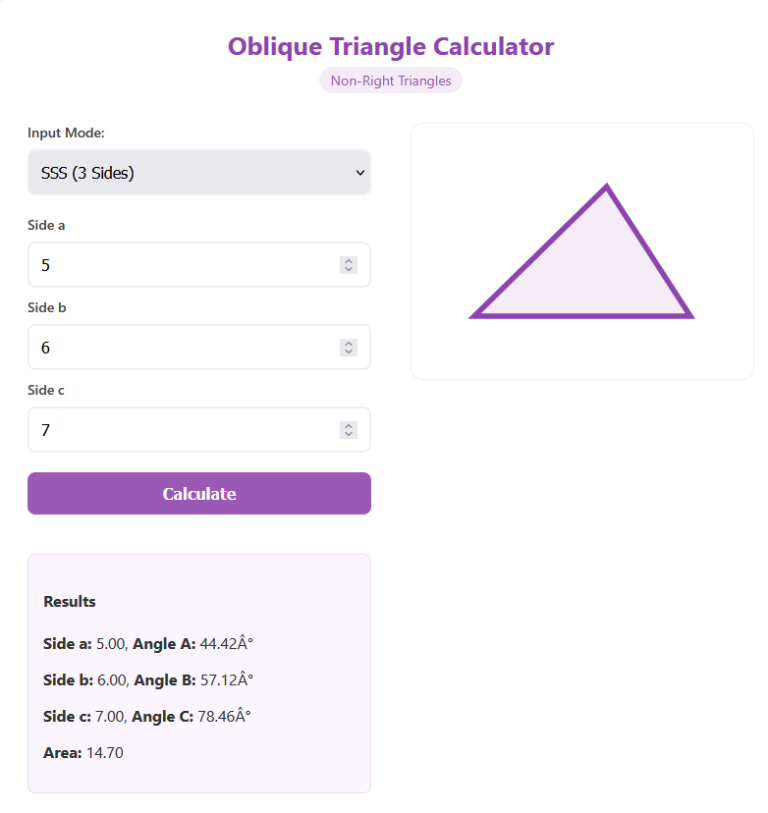
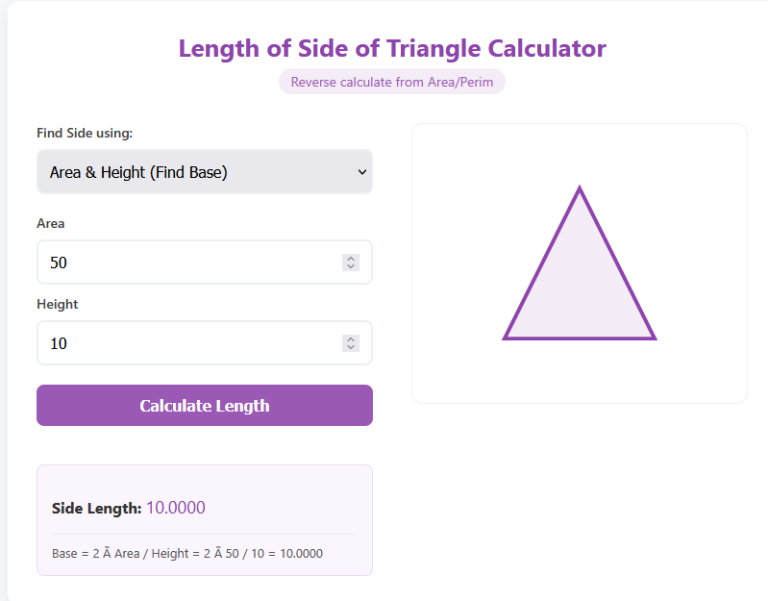
Dynamic Layout: Visualizes the irregular shape to scale.
How to Use This Calculator
Measure Sides: Get the lengths of all three sides (a, b, c).
Input: Enter values into the calculator.
Calculate: Instantly see the Area and Perimeter.
Visualize: The generated image shows how the unequal sides connect.
Formulas
The calculator uses the following mathematical principles:
Semi-Perimeter: $$ s = \frac{a+b+c}{2} $$
Heron’s Formula: $$ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} $$
Perimeter: $$ P = a + b + c $$
Practical Applications
Land Surveying: Calculating the area of irregular plots of land by breaking them into triangles.
Material Estimation: Finding the area of scrap sheets or irregular fabric cuts.
General Geometry: Solving triangles where no height is given.
Tips for Success
Any Triangle: This logic actually works for Equilateral and Isosceles too, but it’s essential for Scalene.
Units: Output is in square units corresponding to the input linear units.
Order: The order of input (a, b, c) does not matter for the area calculation.
Frequently Asked Questions (FAQ)
Do I need the height?
No! That is the beauty of Heron’s Formula; it works on sides alone.
What if the result is 0?
That means the points are collinear (a flat line), not a triangle.
Final Words
Solve the irregular. The Scalene Triangle Calculator handles the complex asymmetry of random triangles with ease, making it the go-to tool for real-world measurements.