Sphere Calculator
Surface Area & Volume for Spheres, Hemispheres & Domes.
Work Shown
The sphere is nature’s masterpiece of efficiency. It is the only shape that encloses the maximum possible volume with the minimum possible surface area. This unique “isoperimetric property” is why water droplets, soap bubbles, and even planets naturally form spheres—forces like surface tension and gravity pull everything into the tightest possible package.
The Sphere Surface Area Calculator is designed to measure the “skin” of this perfect shape. In the real world, calculating this area is critical for everything from manufacturing sports balls to determining the heat loss of a domed building. Whether you are painting a spherical tank, tiling a mosque dome, or solving a geometry problem, knowing the exact surface area is the first step.
Unpacking the Calculator Features
This tool is not just a simple formula plug-in; it is a versatile engineering aid that handles three distinct spherical geometries. Here is how to use each mode:
1. Full Sphere Mode
Use this for complete, round objects like basketballs, marbles, or planets. You only need one measurement:
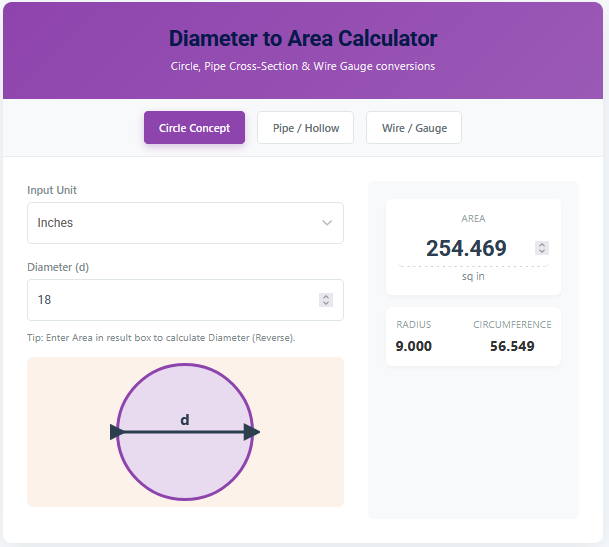
– Radius (): The distance from the center to the edge.
– Diameter (): The distance straight across the middle. If you are measuring a physical object, it is much easier to measure diameter than radius. The calculator accepts either input and instantly updates the other.
2. Hemisphere Mode (Half-Sphere)
Perfect for bowls, domes, or halved fruits. This mode introduces a crucial toggle:
– Include Base Area?: If you check this box, the calculator treats the shape as “Solid” (like a sliced watermelon) and adds the area of the flat circular bottom () to the total. If unchecked, it calculates it as “Hollow” (like an empty bowl), counting only the curved skin.
3. Spherical Cap (Dome) Mode
This is the most advanced feature, designed for architects and fabricators. A “cap” is any slice of a sphere—think of the contact lens shape or a low-profile roof dome. Since you often cannot measure the “radius” of the imaginary full sphere it came from, this mode accepts real-world measurements:
– Dome Base Radius (): The radius of the flat circular footprint of the dome.
– Dome Height (): The vertical distance from the flat base to the highest point (apex) of the dome.
The “Great Circle” Rule
There is a beautiful rule in geometry that makes estimating sphere area surprisingly easy: The surface area of a sphere is exactly 4 times the area of its shadow.
Imagine a tennis ball and its shadow on the ground (a circle). The area of that shadow is the “Great Circle” (). It takes exactly four of those circles to wrap the entire ball perfectly (
). This is why the number 4 appears so prominently in the formula.
Why calculate Sphere Surface Area?
Spheres appear in high-tech engineering and organic nature alike. Here is where these numbers matter:
Architecture and Construction (Geodesic Domes)
Modern marvels like the MSG Sphere in Las Vegas or the Eden Project biomes are massive spherical structures. Architects must calculate the surface area to the square inch to order cladding materials (like LED panels or ETFE cushions). For a dome roof, calculating the “Curved Surface Area” is essential to estimate costs for shingles, copper sheeting, or glass.
Industrial Design (Pressure Vessels)
Fluids and gases under high pressure are often stored in spherical tanks (like those round propane tanks at refineries). Why? Because the sphere distributes stress evenly across every inch of its surface, preventing weak points. Engineers calculate the surface area to determine the specific amount of anti-corrosion paint or thermal insulation required to coat these massive tanks safely.
Biology and Medicine
In biology, the “Surface Area to Volume Ratio” is a matter of life and death. Single-celled organisms, lungs (alveoli), and even heat loss in animals depend on this math. Animals in cold climates tend to be rounder (more spherical) to minimize their surface area (skin) relative to their size, reducing heat loss. This calculator helps students model these biological principles.
Sports Equipment Manufacturing
A FIFA regulation soccer ball must have a precise circumference and surface area to ensure aerodynamic consistency. Manufacturers need to know the exact area of material required for each ball. Since leather or synthetic sheets are flat, they cut them into panels (like pentagons and hexagons) that sum up to the sphere’s total surface area, plus a margin for stitching.
Tips for Accurate Calculation
- **1. Measuring a Physical Sphere**
It is hard to measure the “radius” of a ball because you cannot reach the center. Instead, use a flexible tape measure to find the Circumference (the distance around the middle). Then divide that number by (3.14159) to get the Diameter. Enter that into the calculator for the best accuracy.
- **2. Handling Units**
Always ensure your input units match. If you measure radius in inches, your area will be in square inches (). If you need to paint a dome and the paint coverage is in square feet, convert your result *after* calculation, or convert your input to feet *before* you start.
- **3. The “Hollow” vs. “Solid” Trap**
When calculating for a Hemisphere (like a dome roof), determine if it is “open” or “closed.” A roof is usually hollow (open bottom), so uncheck “Include Base.” A silo cap or a storage tank end might be closed (welded shut), meaning you need to paint the bottom too.
Common Formulas
**Full Sphere:**
**Hemisphere (Curved Part Only):**
**Spherical Cap (Dome) Curved Area:**
Note: The calculator derives the full sphere radius internally to perform this calculation if needed, using .
Frequently Asked Questions (FAQ)
Q: Does the material thickness matter?
A: For surface area, usually no. We assume the “skin” is infinitely thin. However, if the material is very thick (like a concrete wall), you might calculate the “Outer Surface Area” (using the outer radius) and “Inner Surface Area” (using the inner radius) separately to find the difference.
Q: What if I only have the volume?
A: You can work backward! If you know the volume , you can find the radius using . Once you have , you can plug it into this calculator to find the surface area.
Q: Why is a sphere the “most efficient” shape?
A: Mathematically, for any given volume, the sphere has the smallest possible surface area. This means it requires the least amount of material to hold a certain amount of liquid. That is why water drops are round and why beverage cans are cylinders (a compromise between the efficiency of a sphere and the stackability of a box).
Q: Can I use this for non-perfect spheres?
A: If the shape is slightly flattened (like the Earth, which is an oblate spheroid), this calculator gives a very close approximation (usually within 0.3% error for Earth-like scales). For true ovals or eggs (ellipsoids), you need a more complex tool.
Final Words
From the atoms that make up our bodies to the stars that light our sky, the sphere is the fundamental building block of the universe. The Sphere Surface Area Calculator connects you to this geometry, offering the precision needed for complex engineering or simple curiosity. Whether you are building a dome or wrapping a gift, this tool ensures you cover every square inch correctly.