Surface Area Volume Calculator

The Surface Area and Volume (often abbreviated as or ) is a fundamental geometric concept that rules the worlds of biology, chemistry, engineering, and physics. It describes the relationship between the outside skin of an object (surface area) and the amount of space inside it (volume).

As an object gets larger, its volume grows much faster than its surface area. Conversely, as things get smaller (like nanoparticles), their surface area becomes massive relative to their volume. This simple mathematical truth dictates everything from why elephants have big ears to why sugar dissolves faster than rock candy.

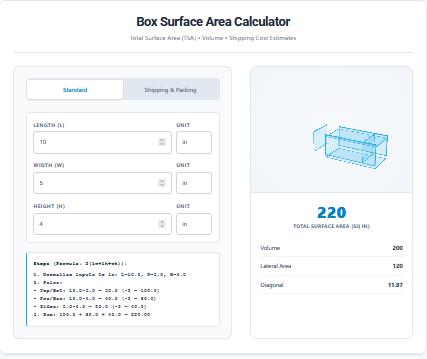
This calculator helps you compute this vital ratio for various geometric shapes like Cubes, Spheres, Cylinders, and Rectangular Prisms, offering instant insights for students, scientists, and engineers.

Key Features of the Calculator

Geometric Versatility

Different shapes behave differently. A sphere has the lowest possible surface area for a given volume, making it the most efficient shape for storing fluids or retaining heat. A flattened sheet or a complex fractal has a huge surface area. Our tool lets you toggle seamlessly between these shapes (Cube, Sphere, Cylinder, Prism) to compare their efficiencies directly.

Dimensional Analysis

Input any dimension—Radius, Side Length, Height—and the tool auto-calculates both the Total Surface Area () and the Volume (), ultimately deriving the quotient . It handles all the complex constants like (Pi) automatically, ensuring high-precision results.

Visualizing Scale (The Square-Cube Law)

The tool is excellent for demonstrating the “Square-Cube Law”. You can enter a side length of 1, then 2, then 10, and watch the Ratio plummet. This visual feedback is crucial for students trying to grasp why cells divide instead of just growing forever. Doubling the size differs the area by 4x but the volume by 8x, halving the ratio.

Scientific & Practical Applications

Biology: The Limits of Cell Size

Cells rely on diffusion to move nutrients (like oxygen) in and waste (like ) out. This occurs across the cell membrane (Surface Area). If a cell gets too big, its Volume (metabolic needs) outpaces its Surface Area (supply lines), and it dies. High is critical for survival at the cellular level. This is why most cells are microscopic; they maximise their surface contact with the environment.

Zoology: Allen’s Rule & Bergmann’s Rule

Animals in cold climates tend to be larger and rounder (low ) to conserve heat (e.g., Polar Bears, Walruses). Animals in hot climates need to shed heat, so they are often smaller or have large appendages to increase surface area (e.g., the Fennec Fox’s massive ears or the African Elephant’s ears). This evolutionary traits are direct consequences of ratios.

Chemical Engineering: Catalysis

Chemical reactions often happen on the surface of a solid catalyst. To speed up a reaction, engineers powderize the catalyst. Why? Because a pile of powder has a staggeringly higher ratio than a single solid block of the same mass, offering more “sites” for the reaction to occur. This is how catalytic converters in cars work.

Nanotechnology

At the nanoscale (1-100 nm), the ratio becomes so extreme that materials start behaving differently. Gold, usually inert, becomes highly reactive. This dominance of surface atoms over bulk atoms is the driving force behind the entire field of nanoscience.

Heat Transfer & Cooking

Why do french fries cook faster than a baked potato? Ratio. The thin strips of potato have a huge surface area exposed to the hot oil relative to their small volume, allowing heat to penetrate instantly. A round roast (low ) takes hours because the heat has to travel deep into a large volume through a relatively small surface.

Formula Cheat Sheet

• Sphere (Most Efficient): , . Ratio = . Notice clearly: as increases, the ratio decreases inversely.

• Cube: , . Ratio = . Similar to the sphere, efficiency drops as size () grows.

• Cylinder: , . Ratio varies by shape factor. A long thin wire has high SA:V; a short squat “hockey puck” has lower SA:V.

Tips for Inputs

Ensure your units are consistent. If you measure radius in cm, your Area is and Volume is . The Ratio unit will be “inverse length” (). If you mix inches and feet, your ratio will be meaningless.

Frequently Asked Questions (FAQs)

1. What is the standard unit of SA:V Ratio?

The unit is always inverse length (), such as , , or . It represents how much surface area exists per unit of volume. A value of “2 ” means there are 2 square centimeters of surface for every 1 cubic centimeter of volume.

2. Which shape has the best SA:V ratio?

It depends on what you mean by “best”. For *minimizing* surface area (storing things like water or gas), the Sphere is best. For *maximizing* surface area (radiators, heat sinks, absorption), complex shapes with fins, folds, or fractals are best.

3. Why do babies get cold faster than adults?

Babies are smaller, meaning they have a significantly higher Surface Area to Volume Ratio. They lose body heat through their skin much faster relative to their total body mass impacting their ability to thermoregulate. This is why swaddling is important.

4. How does this apply to packaging?

To save money on cardboard (Surface Area) while shipping the most product (Volume), companies should ideally use spherical boxes. Since spheres don’t stack well on pallets, cubes or cuboids are the next best compromise, minimizing material costs.

5. Is a higher ratio always better?

No. It is a trade-off. High ratio is good for reaction speed, cooling, and dissolving. Low ratio is good for insulation, storage capacity, and stability.

Conclusion

From the nano-structures of activated charcoal to the cooling of stars, the Surface Area to Volume Ratio is a governing number of the universe. It explains the design of our lungs (millions of tiny alveoli), the shape of cactus leaves, and the efficiency of industrial reactors. Use this standard calculator to bridge the gap between abstract geometry and real-world efficiency.