Triangle Area Calculator Using Heron’s Formula
Heron’s Formula:
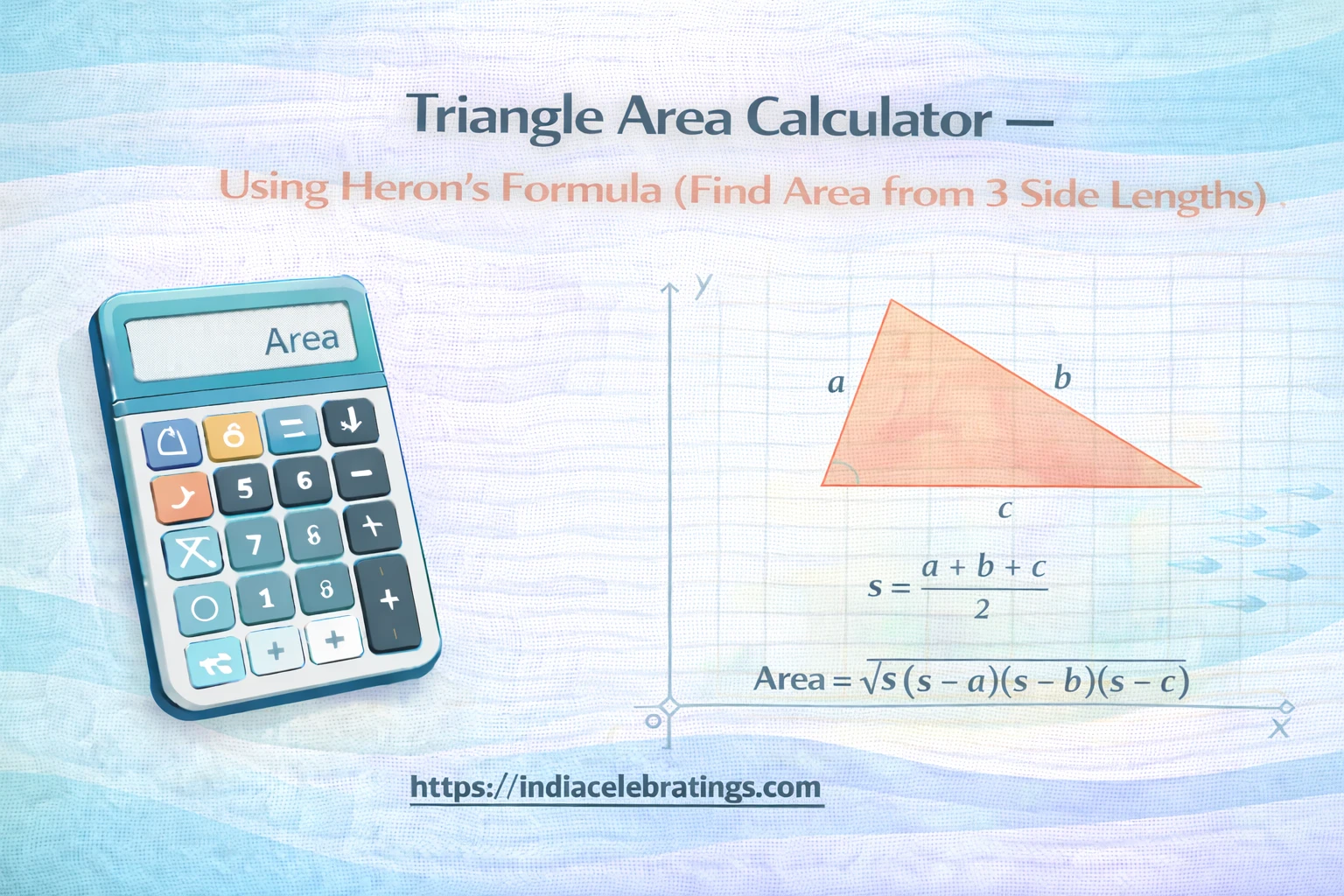
s = (a + b + c) / 2
Area = √[s (s − a) (s − b) (s − c)]
In geometry, you often need to find the area of a triangle. When the base and height are known, the calculation is easy. But what if you only know the three side lengths? In many real-world problems, the height is not given or is hard to measure.
This is where Heron’s Formula becomes very useful. A Triangle Area Calculator using Heron’s Formula allows you to find the area of any triangle using just the three sides. You do not need angles, heights, or coordinate points.
By simply entering the side lengths, the calculator applies the correct formula and gives you the area instantly. This makes it perfect for students, engineers, surveyors, and anyone working with triangle measurements.
What Is a Triangle Area Calculator Using Heron’s Formula?
A Triangle Area Calculator using Heron’s Formula is an online geometry tool that calculates the area of a triangle when all three sides are known.
What Is Heron’s Formula?
Heron’s Formula is a mathematical method used to find the area of a triangle without using height or angles. It only needs the side lengths.
What the Calculator Can Find
The calculator determines:
The semi-perimeter of the triangle
The area using Heron’s Formula
Whether the triangle is valid based on side lengths
It works for scalene, isosceles, and acute or obtuse triangles.
How the Calculator Works
The calculator follows a simple step-by-step process.
Step 1: Enter the Three Side Lengths
You provide:
Side a
Side b
Side c
Step 2: Check Triangle Validity
The calculator checks the triangle inequality rule:
The sum of any two sides must be greater than the third side.
Step 3: Calculate the Semi-Perimeter
Half of the perimeter is calculated.
Step 4: Apply Heron’s Formula
The formula is used to compute the area.
Step 5: Display the Area
The final result is shown instantly.
Key Formulas Used in the Calculator
Semi-Perimeter Formula
s = \frac{a + b + c}{2}Heron’s Formula for Area
\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}These formulas work for all valid triangles.
Step-by-Step Examples
Example 1: Simple Triangle
Side lengths:
a = 5 units
b = 6 units
c = 7 units
Semi-perimeter:
s = \frac{5 + 6 + 7}{2} = 9Area:
\text{Area} = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} \text{Area} = \sqrt{216} \approx 14.7Example 2: Isosceles Triangle
Side lengths:
a = 8 units
b = 8 units
c = 6 units
The calculator completes these steps instantly.
Features of the Triangle Area Calculator
Only Three Inputs Required
No need for angles or heights.
Automatic Validity Check
Ensures the sides form a real triangle.
Instant Results
Area is calculated in seconds.
Works for All Triangle Types
Scalene, isosceles, acute, or obtuse.
Simple Interface
Easy for beginners and professionals.
Uses and Applications of the Calculator
Student Learning
Students use this calculator to solve geometry homework and verify answers using Heron’s Formula.
Engineering and Construction
Engineers use triangle areas for structural design, material estimation, and planning.
Surveying and Land Measurement
Surveyors calculate areas of triangular land sections using side lengths.
Architecture and Design
Designers use triangle geometry in layouts and structural planning.
Tips to Avoid Common Mistakes
One common mistake is entering side lengths that do not satisfy the triangle inequality rule. Always ensure the sum of any two sides is greater than the third.
Another error is rounding the semi-perimeter too early. Keep full values until the final calculation.
Some users confuse Heron’s Formula with the base-height formula. Remember that Heron’s Formula does not use height at all.
Be careful with units. If sides are in meters, the area will be in square meters.
Finally, always double-check your input values before calculating.
Frequently Asked Questions (FAQs)
What is Heron’s Formula?
A formula used to find triangle area using only side lengths.
Do I need the height of the triangle?
No. Heron’s Formula does not require height.
Does it work for all triangles?
Yes, as long as the sides form a valid triangle.
What units does the area use?
Square units based on the side length units.
Is the calculator accurate?
Yes, it uses standard geometry formulas.
Final Words
The Triangle Area Calculator using Heron’s Formula is a powerful and reliable tool for finding the area of a triangle when only the side lengths are known. It removes the need for height or angle measurements and delivers fast, accurate results.
Whether you are a student, engineer, or surveyor, this calculator helps you solve triangle area problems with confidence and ease.
