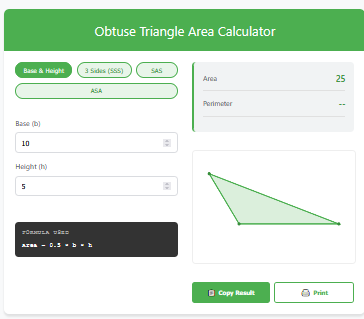
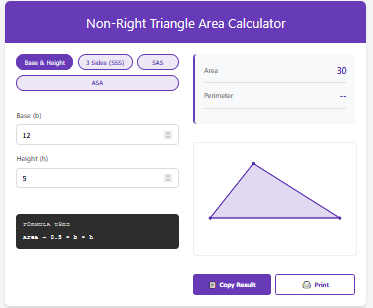
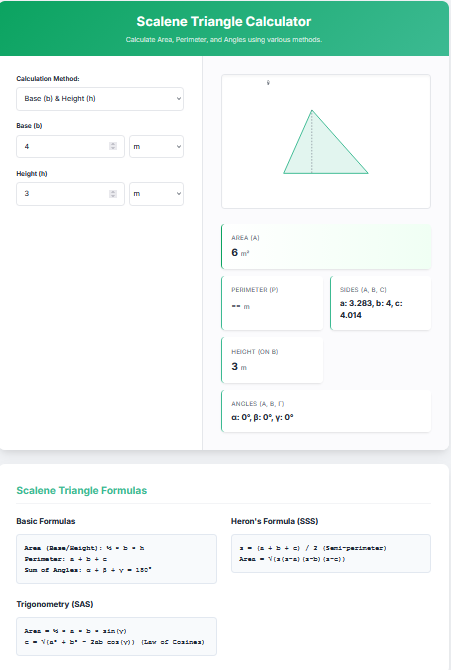
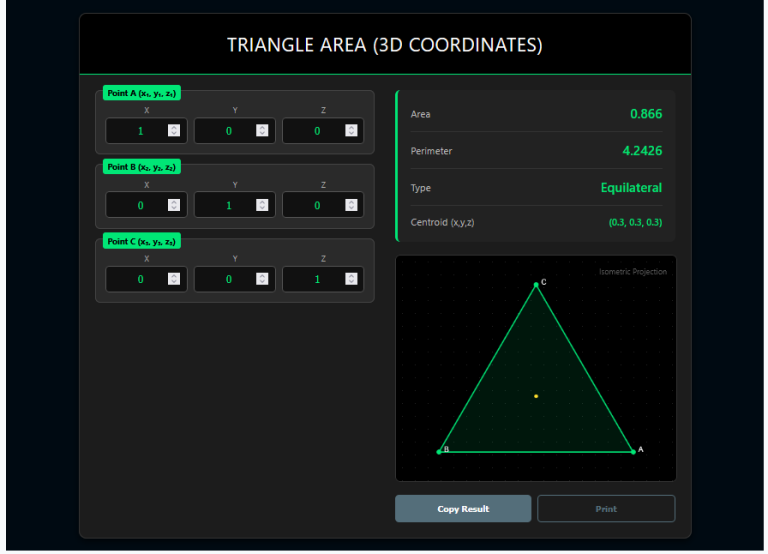
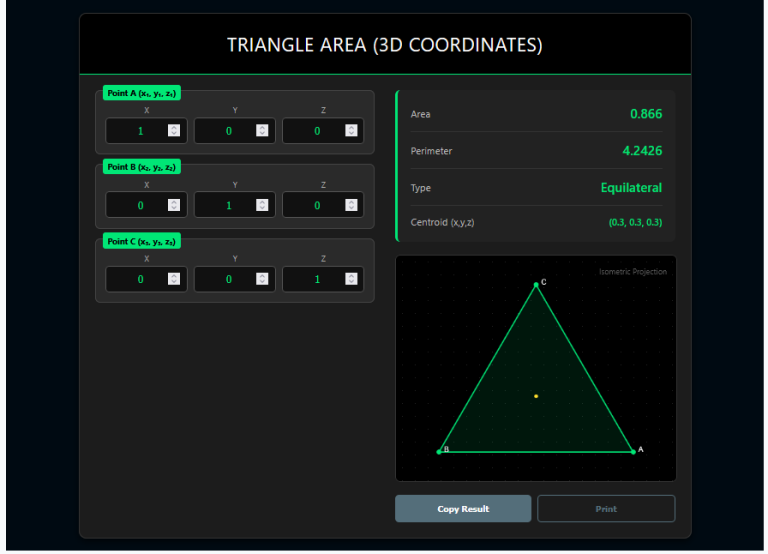
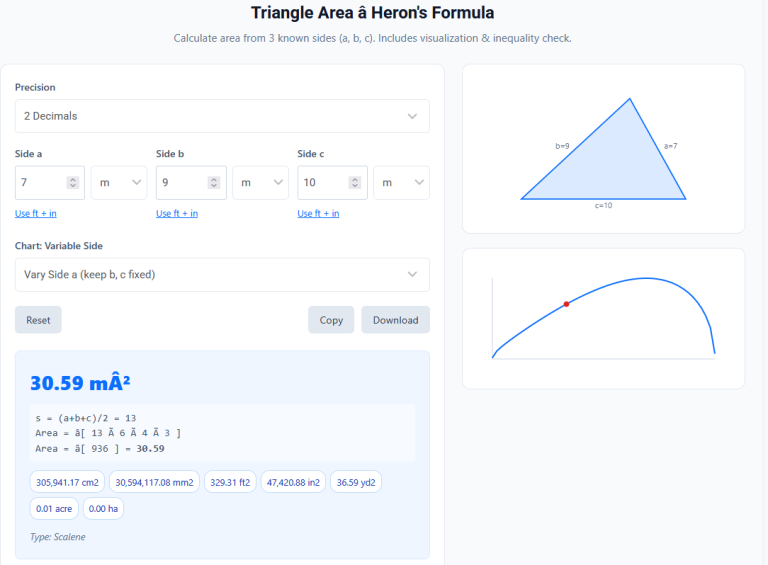
The Triangle Area Using Vectors Calculator is a specialist tool that skips the geometry of “sides” and “angles” and works directly with the pure math of Magnitude and Direction.
It is designed for physics students and engineers who define shapes not by where they are (points) but by how they span space (vectors).
Calculator Features
1. Direct Vector Input
Enter your two vectors $\vec{u}$ and $\vec{v}$ directly using their $i, j, k$ components. No need to calculate endpoints first.
2. Cross Product Visualization
The tool computes the cross product vector ($\vec{w} = \vec{u} \times \vec{v}$) and calculates its magnitude, which represents the area of the parallelogram formed by the vectors.
3. Unit Normal Calculation
Examples often require finding the “normal vector” (perpendicular to the surface). This calculator provides that unit vector automatically.
4. 2D & 3D Flexibility
Whether your vectors are flat on a page (2D) or pointing through space (3D), the math engine adapts instantly.
The Area Formula
The area of a triangle formed by two vectors is exactly half the magnitude of their cross product:
Area $A = \frac{1}{2} |\vec{u} \times \vec{v}|$
Cross Product Components
For vectors $\vec{u} = \langle u_x, u_y, u_z \rangle$ and $\vec{v} = \langle v_x, v_y, v_z \rangle$:
$\vec{u} \times \vec{v} = \langle (u_y v_z – u_z v_y), (u_z v_x – u_x v_z), (u_x v_y – u_y v_x) \rangle$
Magnitude Calculation
The final area calculation uses the Pythagorean distance of the resulting vector components:
$|\vec{u} \times \vec{v}| = \sqrt{c_x^2 + c_y^2 + c_z^2}$
Real-World Applications
Electromagnetism
In physics, calculating magnetic flux often requires finding the area vector of a surface loop. This calculator does exactly that.
Computer Graphics (Lighting)
To calculate how light bounces off a 3D triangle, the computer needs the “Normal Vector,” which this calculator derives from the cross product.
Aerodynamics
Engineers use vector areas to calculate Lift and Drag forces acting on specific triangular panels of an aircraft wing.
Tips
Tail-to-Tail
Ensure your two vectors originate from the same point (tail-to-tail). If they are head-to-tail, the magnitude (Area) is correct, but the Direction (Normal) might be flipped.
Zero Area?
If you get an area of 0, it means your two vectors are parallel (pointing in the same or opposite direction). They don’t form a triangle; they form a line.
Frequently Asked Questions (FAQs)
1. What is i, j, k?
These are the standard unit vectors along the axes:
$i$ = x-axis direction
$j$ = y-axis direction
$k$ = z-axis direction
2. Why divide by 2?
The magnitude $|\vec{u} \times \vec{v}|$ gives the area of a PARALLELOGRAM. Since a triangle is half of a parallelogram, we divide by 2.
3. Can I use negative components?
Absolutely. Vectors have direction, so negative numbers just mean pointing “backwards” along an axis. The math handles it comfortably.
Final Words
The Triangle Area Using Vectors Calculator is a specialized instrument for the mathematically inclined. By stripping away coordinate geometry and focusing purely on vector spans, it offers the fastest path to solving problems in physics, engineering, and higher-level calculus.