Triangle Area Calculator Using Vectors
Vector A
Vector B
Formula:
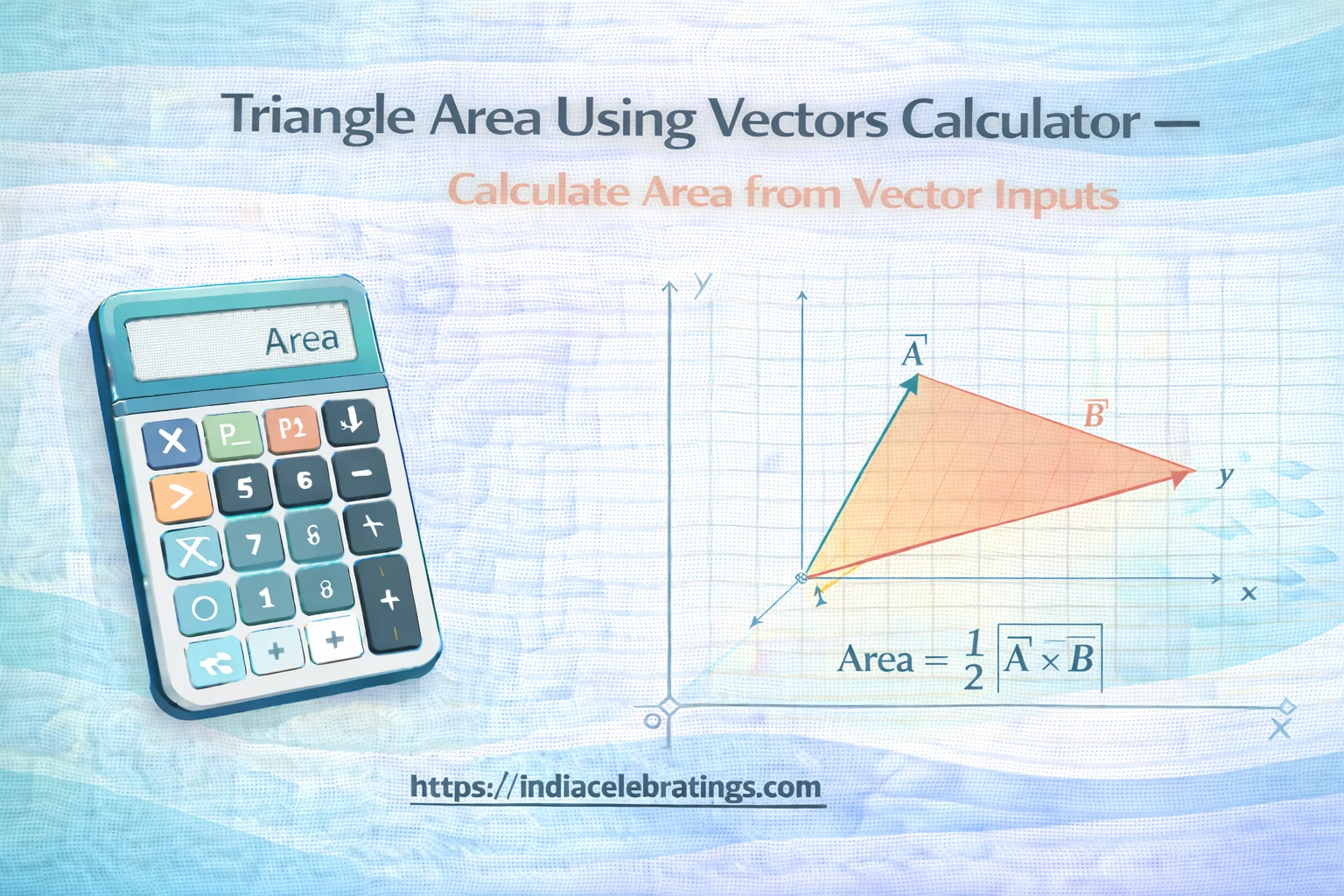
Area = ½ × |A × B|
In 2D: ½ × |Ax·By − Ay·Bx|
In 3D: ½ × |cross product magnitude|
In mathematics, physics, and engineering, vectors are used to represent quantities that have both magnitude and direction. When two vectors form a triangle, we can find the area of that triangle using vector operations instead of traditional geometry formulas.
A Triangle Area Using Vectors Calculator makes this process fast and simple. Instead of entering side lengths or angles, you only need to enter the components of two vectors. The calculator then uses the cross product to find the triangle’s area.
This method is especially useful in 2D and 3D problems, computer graphics, physics, and engineering calculations.
What Is a Triangle Area Using Vectors Calculator?
A Triangle Area Using Vectors Calculator is a math tool that finds the area of a triangle formed by two vectors using vector mathematics.
How a Triangle Is Formed from Vectors
When two vectors start from the same point:
They form a parallelogram
The triangle is half of that parallelogram
So, the triangle’s area is half the area of the parallelogram created by the two vectors.
What the Calculator Can Find
The calculator determines:
Area of the triangle
Cross product of the vectors
Magnitude of the cross product
Direction of the normal vector (in 3D cases)
This makes it useful for both learning and advanced calculations.
How the Calculator Works
The calculator follows a clear vector-based process.
Step 1: Enter Vector Components
You enter:
Vector u components: (u_x, u_y, u_z)
Vector v components: (v_x, v_y, v_z)
These can be 2D or 3D vectors.
Step 2: Compute the Cross Product
The calculator finds the cross product of the two vectors.
Step 3: Find the Magnitude
The length of the cross product vector is calculated.
Step 4: Divide by 2
Half of the magnitude gives the area of the triangle.
Key Formulas Used in the Calculator
Cross Product of Two Vectors
\vec{u} \times \vec{v} = \langle u_y v_z - u_z v_y,; u_z v_x - u_x v_z,; u_x v_y - u_y v_x \rangleThis creates a vector perpendicular to both (\vec{u}) and (\vec{v}).
Magnitude of a Vector
|\vec{w}| = \sqrt{w_x^2 + w_y^2 + w_z^2}This gives the length of the cross product vector.
Triangle Area Using Vectors
\text{Area} = \frac{1}{2} |\vec{u} \times \vec{v}|This formula gives the area of the triangle formed by the two vectors.
Step-by-Step Example
Example 1: 2D Vectors
Let:
(\vec{u} = (4, 2, 0))
(\vec{v} = (1, 3, 0))
Step 1: Find Cross Product
\vec{u} \times \vec{v} = \langle 0, 0, (4 \times 3 - 2 \times 1) \rangle \vec{u} \times \vec{v} = \langle 0, 0, 10 \rangleStep 2: Find Magnitude
|\vec{u} \times \vec{v}| = \sqrt{10^2} = 10Step 3: Find Triangle Area
\text{Area} = \frac{1}{2} \times 10 = 5So, the triangle area is 5 square units.
Example 2: 3D Vectors
Let:
(\vec{u} = (2, 1, 3))
(\vec{v} = (1, 4, 2))
Step 1: Cross Product
\vec{u} \times \vec{v} = \langle (1\times2 - 3\times4), (3\times1 - 2\times2), (2\times4 - 1\times1) \rangle \vec{u} \times \vec{v} = \langle -10, -1, 7 \rangleStep 2: Magnitude
|\vec{u} \times \vec{v}| = \sqrt{(-10)^2 + (-1)^2 + 7^2} = \sqrt{150}Step 3: Triangle Area
\text{Area} = \frac{1}{2} \times \sqrt{150} \approx 6.12The calculator performs all these steps instantly.
Features of the Triangle Area Using Vectors Calculator
Supports 2D and 3D Vectors
The calculator works for both planar and spatial vectors.
Automatic Cross Product Calculation
You do not need to compute vector products manually.
Instant Area Results
The final triangle area is shown in seconds.
Normal Vector Display
In 3D, the perpendicular direction can also be shown.
Simple Input System
Only vector components are required.
Uses and Applications of the Calculator
Physics Problems
In physics, vectors represent forces, velocity, and displacement. This calculator helps find areas related to vector diagrams and torque problems.
Engineering Calculations
Engineers use vector geometry for structural analysis, motion design, and force systems. The calculator saves time and reduces errors.
Computer Graphics and 3D Modeling
Triangle areas are important for rendering, shading, and mesh design. Vector-based area calculations are widely used in graphics engines.
Mathematics Education
Students use this tool to understand cross products and vector geometry clearly.
Tips to Avoid Common Mistakes
One common mistake is entering vector components in the wrong order. Always make sure (u_x, u_y, u_z) and (v_x, v_y, v_z) are placed correctly.
Another frequent error is forgetting to include the third component in 2D problems. Use 0 for the z-value when working in two dimensions.
Some users confuse dot product with cross product. The dot product does not give area. Only the cross product is used for triangle area.
Rounding too early can reduce accuracy. Keep full decimal values until the final result.
Finally, make sure both vectors start from the same point. Otherwise, they will not form the correct triangle.
Frequently Asked Questions (FAQs)
What is the cross product?
It is a vector operation that produces a vector perpendicular to two given vectors.
Why is the area divided by 2?
Because a triangle is half of a parallelogram formed by two vectors.
Can I use this for 2D vectors?
Yes, just use 0 for the z-component.
Is this method accurate?
Yes, it is a standard mathematical method.
What units does the area use?
The units depend on the units of the vector components.
Final Words
The Triangle Area Using Vectors Calculator is a powerful and efficient tool for finding triangle areas using vector mathematics. By applying the cross product formula, it avoids complex geometric constructions and delivers accurate results instantly.
Whether you are a student, engineer, or graphics designer, this calculator helps you solve vector-based triangle problems with confidence and ease.
